- Which is the relation between logic and mathematics? Does logic constitute the foundations of mathematics (is all mathematics a result of logical application), or is logic a part of mathematics (or neither nor)?
- Another question concerns the Law of the Excluded Middle (LEM). How can we look upon this basic logical law if we apply it on propositions that lack meaning?
- Which are the metaphysical and ontological consequences of regarding LEM as being a universal natural law?
Meaning and logic
A proposition lacks meaning when we have no possibility to settle its truth value. To this category of propositions belong those for which we do not have, or cannot have, any fact that can render the proposition a truth value. This is the case for many metaphysical propositions. Also mathematical propositions can lack meaning. This is the case for valid conclusions based on premises that have no justification (mathematically or otherwise), but are present only as postulated and arbitrary propositions. For mathematical propositions to be menaingful we need that all presented premises can be derived to the basic axiom (the natural numbers and their well-ordering), the operators (calculation methods) and also the induction principle as well as recursive definitions. This means that all mathematical propositions are logical truths (verified only by derivation from true premises, not by empirical evidence). Here we will say that logical truth are meaningful as they are possible to verify, but sometimes a stronger distinction between logical and empirical truths is used, where only propositions that are empirically possible to verify are regarded as meaningful (and then logical truths are regarded as meaningless).
Now, LEM says that a proposition is either true or false, there is no third alternative. This entails that there is no such thing as a meningless proposition. The inventor of logic, Aristotle, thought for instance that propositions about the outcome of the sea-battle tomorrow are all true or false, although we do not yet know which of the two. These thoughts have had great impact on our thinking since then. But today, we can se in logic, that there is a difference between valid and sound arguments, namely that a valid but unsound argument has a false premise (although the argument itself is valid). If a premise has the property of having no evidence, then it is fatal to hold this premise as either true or false, because the conclusion will, in a sort of unvisible way, be as meningless as the premise. There is a difference between not being false and being true. This difference is not acknowledged by any reasoning involving LEM. And if we accept premises that have no evidence, then we can always, and without any means to prevent it, interchange such a premise to one that contradicts the original one, with a totally different conclusion as a result. Such a premise is merely a matter of belief and arbitrary reasoning. It undermines logic. This is not a problem with LEM, but a problem of its application. We must acknowledge the existence of meaningless propositions (although it is not necessary to call them propositions). And LEM cannot be applied onto meaningless propositions. Beware; the concept of lacking meaning is more basic than the fact that LEM is not a universal law. That fact is caused by the nature of meaningless propositions.
These considerations affect the concept of proof by contradiction. If we have no LEM, then we have to exclude all mathematical results obtained by this kind of proof. But, again, it not a question of doubting LEM, it is a question of doubting its universality (or rather of doubting the non-existance of meaningless mathematical propositions, which are the cause of lack of universality of LEM), and where results are obtained on the basis of meaningless premises we would be better off without these particular results (e.g. the theory of transfinite numbers). A premise without meaning cannot be a part of a logical argument whose conclusion have a meaning. Or: the conclusion will never have more meaning than the premises, by purely logical reasons. This is investigated in the essay Richard´s paradox – impredicativity and infinity coinciding.
Mathematics and logic
When considering the relation between logic and mathematics the circumstances mentioned above it clearly is relevant that logical operations are used to render mathematical propositions a meaning and thus a truth value, and thus it might be reasonable to regard logic as more basic than mathematics. However, this is not a totally apparent conclusion when considering the origins of logic. We will come back to this investigation later.
Here is an essay that treats Russell´s paradox from a logical perspective (in Swedish):
This essay exposes the reasons why the following is a logical truth (A is a set):
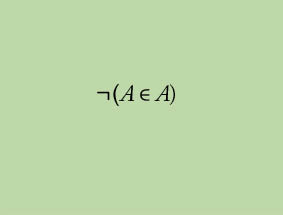
Those reasons are dissolving Russell´s paradox in terms of what we restrict ourselves to be able to do logically when we apply an asymmetric relation between two objects.
(The text above is subject to ongoing changes. (Updated 27th June 2021)